哈希
2023/9/15
原文链接:Hashing
作为一个程序员,你几乎每天都会使用哈希函数。哈希函数被用在数据库中优化数据查询,也被用于一些数据结构以优化性能,更可以用于安全领域来保障数据安全。你所使用的几乎每个技术都会以某种方式使用哈希。
哈希函数是非常基础的,它无处不在。
但,什么是哈希函数,它是如何运作的?
在本篇文章中,我们会向你揭晓哈希函数的运作。我们会从最简单的哈希函数开始,然后学习对哈希函数的测试,最后我们会聚焦于哈希函数的实际应用:哈希表。
什么是哈希函数?
哈希函数是一种接受一个输入(通常是一个字符串),根据这个输入返回一串数字的函数。如果你多次以同一参数调用哈希函数,它会返回同一串数字,并且这串返回的数字必定在预期的范围内。这里的范围取决于哈希函数的实现,有的哈希函数使用 32 位整型(0 到 四十亿),其它的可能会更大。
让我们使用 JavaScript 写一个伪哈希函数,它看起来应该像这样:
function hash(input) {
return 0;
}
即使不知道这个哈希函数应该如何使用,但它肯定不是无用的。接下来让我们看看一个好的哈希函数如何编写,在这之后,我们会探寻哈希函数在哈希表中的使用。
怎样的哈希函数更好?
由于函数的输入可以是任何字符串,但返回的数字则是在一定范围内的,这就导致两个不同的输入可能导致相同的输出,这被称为“哈希碰撞”。而一个好的哈希函数应该应可能的减少哈希碰撞的产生。
完全阻止哈希碰撞的产生是不可能的。如果我们编写一个返回值范围在 0 到 7 的哈希函数,然后给予它九个不同的输入,我们会发现至少一次哈希碰撞。
hash("to") == 3
hash("the") == 2
hash("café") == 0
hash("de") == 6
hash("versailles") == 4
hash("for") == 5
hash("coffee") == 0
hash("we") == 7
hash("had") == 1
上述这些输出值来自 8 的模数。无论哪 9 个数作为输入,返回值只会是 0 到 7 这 8 个数。也因此,哈希碰撞是不可避免的,而我们的目标就是使碰撞尽可能地减少。
为了可视化哈希碰撞,我使用了一个网格。网格中的每一个格子都用来表示哈希函数输出的一个数。这里是一个 8x2 的网格(见原文)。点击网格以进行示例哈希函数输入的累加,并且你可以看到我们将其映射进网格的格子中。观察当输入值大于网格数量时会发生什么。
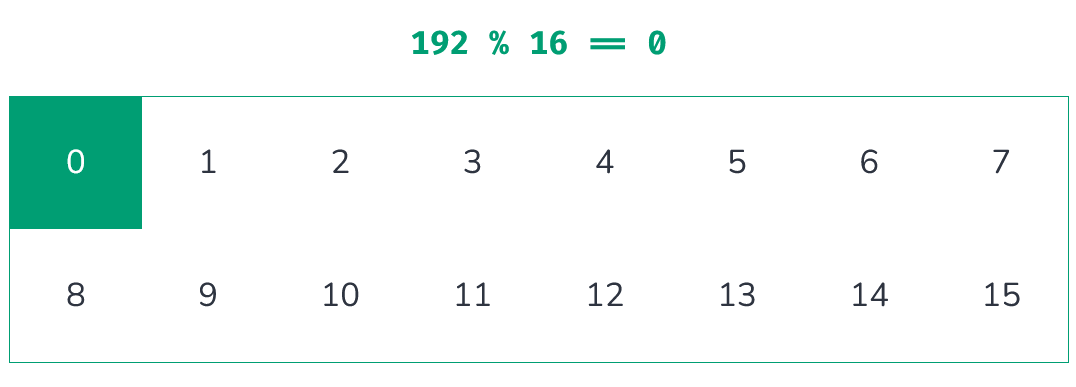
每一次我们计算一个值的哈希,我们都让其相应的方格的颜色变深。这个方法创造了一个简单的方式让我们来观察一个哈希函数是如何阻止哈希碰撞的。我们在探索的是更好地让结果均匀分布到每一个方格中的方法。通过这个方法我们会发现某个不足够可用的哈希函数。
Haskie:文中提到,当一个哈希函数对于两个不同的输入输出相同的值的情况称为哈希碰撞。
但如果我们的哈希函数的输出值在一个非常大的范围内,我们再将那些范围映射到一个小网格中,这不就是在本无碰撞的网格中创造哈希碰撞吗?
在前面的 8x2 网格中,1 和 17 都被映射到第二个网格中。
这很对,我们正在我们的网格中创造“伪碰撞”。这没什么,因为即使是对于最好的哈希函数也会出现多重分配的情况。在每一个方格上累加 100 与累加 1 是一样好的分配方式。如果我们有一个常常出现碰撞的不良的哈希函数,那会变得很明显。
让我们创建一个更大的网格并且用这个网格表示 1000 个随机生成的字符串。你可以点击这个网格(见原文)以计算新的随机输入的集合的哈希,这个网格会通过动画展示每一个输入的哈希计算结果并体现在网格中。

这些值很好地被平均分配了,这是因为我们使用了广为人知的哈希函数 murmur3。这一哈希函数因其高性能和良好的分配性被广泛运用。
如果我们使用了一个不好的哈希函数,我们的网格会是什么样?
function hash(input) {
let hash = 0;
for (let c of input) {
hash += c.charCodeAt(0);
}
return hash % 1000000;
}
这个哈希函数遍历输入的字符串并且计算求和每一个字符对应的数值。通过取模运算符 % 来将结果限制在 0 到 1000000 之间。我们可以把这个哈希函数称作 stringSum。
这个网格是由 1000 个随机生成的字符串哈希运算形成的。

这似乎与 murmur3 产生的效果差不多。
有个问题,这些输入的字符串是随机产生的。让我们看看对于固定的字符串:从 1 到 1000 的数字转化成的字符串,这两个方法(murmur3 和 stringSum)的表现如何。

现在问题明晰了。当输入不随机时,stringSum 的输出呈现出一个模式;而我们的 murmur3 网格,则看起来和使用随机值时相同。
如果我们对使用率前 1000 的英语单词进行哈希运算,结果如下:

这张图不是很明显,但我们仍然可以在 stringSum 的网格中看到一定的规律,但 murmur3 的网格则与之前看到的相近。
这就是一个好的哈希函数应具有的能力:不管输入如何,输出都是平均分布的。让我们再讨论另一种可视化的方法并且说明其的重要性。
雪崩效应
另一种测试哈希函数的方法被称为“雪崩效应”。这指的是当输入中有一个 bit 发生变化时,输出中会有多少个 bit 改变。对于一个好的哈希函数(其具有足够的雪崩效应),输入中一个 bit 的变化会导致输出中平均半数的 bit 发生改变。
这是一个能够阻止哈希函数在网格中形成规律的一个重要的属性。如果输入中小的变化会导致输出中的微笑改变,这个哈希函数的规律就会很容易被发现。而规律意味着较低的分配率和较高的哈希碰撞率。
在下面,我们通过展示两个 8-bit 二进制数字来可视化雪崩效应(见原文)。图片中上面的一行为输入,下面一行为哈希函数的输出。点击它以翻转输入中的一个 bit,输出中变化的 bit 会变为绿色,不变的 bit 会变为红色。
这是 murmur3 的结果:
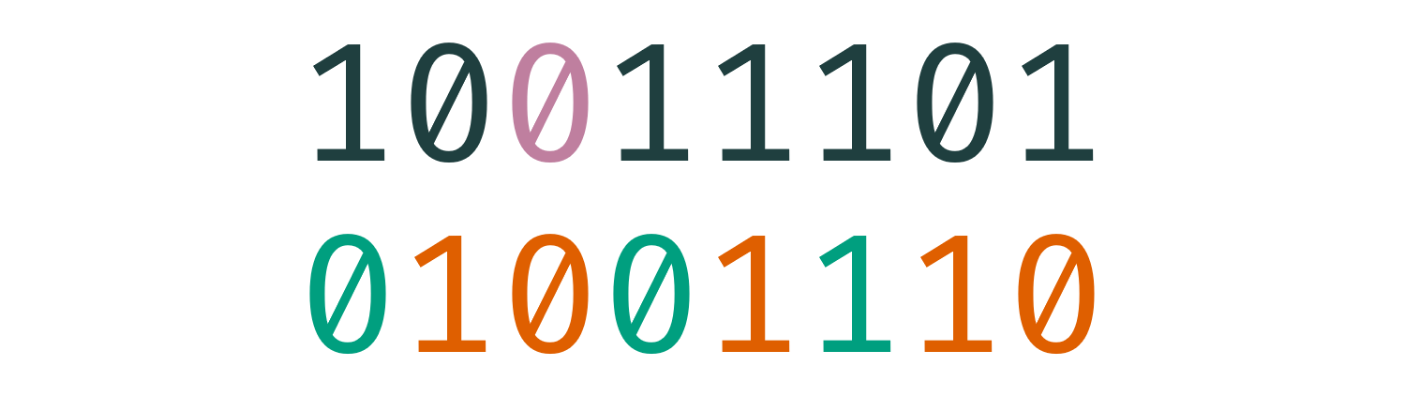
murmur3 做得很好,虽然你可能注意到了,一些时候变化的 bit 的数量并不是刚好的 50%,有时略小于有时略大于。这也无伤大雅,这说明它具有平均 50% 的翻转率。
让我们看看 stringSum 的表现:
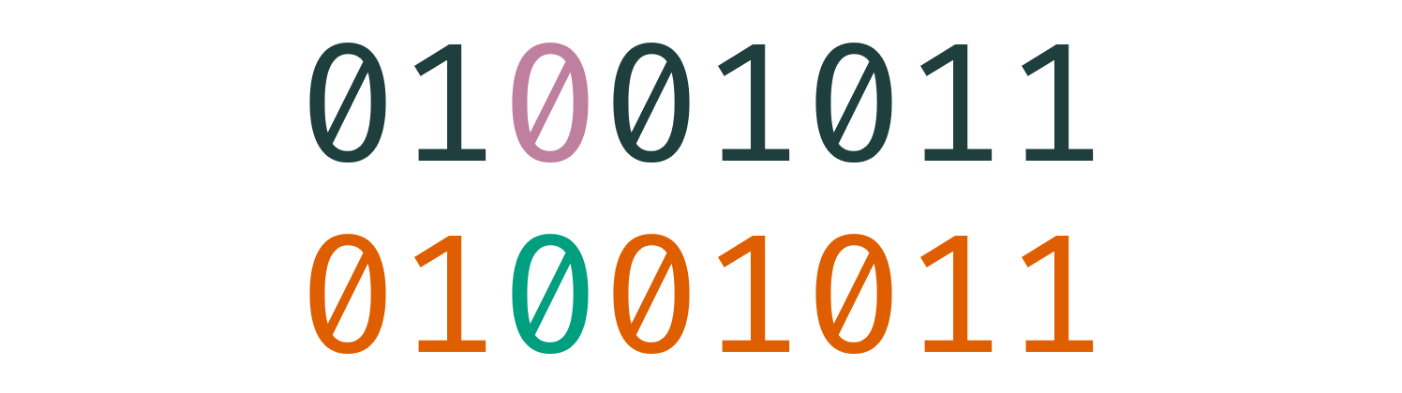
这个结果并不理想。可以看到,下面的输出等同于上面的输入,因此每次输入变化,在输出中仅有一个 bit 发生翻转。这也不难理解,因为 stringSum 函数仅仅求和了字符串中每一个字符对应的数字值。在这个例子中,stringSum 相当于只计算了一个字符,这意味着输出总是会和输入相同。
导致这一结果的原因
我们花费了一些时间来理解这些评估哈希函数优劣的方式,但我们还没有解释这些方法起作用的原因。让我们通过哈希表来说明这一点。
想要理解哈希表,我们首先需要理解表是什么。表是一种允许你存储键值对的数据结构。下面是一个 JavaScript 的代码示例:
let map = new Map();
map.set("hello", "world");
console.log(map.get("hello"));
在上面的代码中,我们定义了一个键值对 "hello" -> "world" 并且将其存储到表中。然后我们打印了键 "hello" 对应的值,即 "world"。
判断 anagram 可能会是一个更有趣的实际用例。anagram 是两个不同的包含相同的字母的单词,例如 "antlers" 和 "rentals" 或者 "article" 和 "recital"。如果你有一些单词,你想要找出其中所有的 anagram,你可以按字母表顺序排序,再用其作为表中的键。
let words = [
"antlers",
"rentals",
"sternal",
"article",
"recital",
"flamboyant",
]
let map = new Map();
for (let word of words) {
let key = word
.split('')
.sort()
.join('');
if (!map.has(key)) {
map.set(key, []);
}
map.get(key).push(word);
}
这段代码的结构会是如下结构的一张表:
{
"aelnrst": [
"antlers",
"rentals",
"sternal"
],
"aceilrt": [
"article",
"recital"
],
"aabflmnoty": [
"flamboyant"
]
}
实现你自己的简易哈希表
哈希表是众多表的实现中的一种,并且存在有多种方式来实现。最简单的方式,就是使用一个数组的数组。其中内层的数组在现实中通常被称作“桶”,因此我们也这样在此称呼它。哈希函数被用于键以计算应该使用哪一个桶来存储这一键值对。
让我们用 JavaScript 来简单实现一个哈希表。我们准备自下而上来进行实现,所以在我们开始实现 set 和 get 函数之前,我们会先看到一些工具函数的实现。
class HashMap {
constructor() {
this.bs = [[], [], []];
}
}
我们从创建 HashMap 类开始,在构造函数中初始化了三个桶。我们只使用了三个桶还有简短的变量名 bs,这样这些代码能够更好地展现在小屏设备中。在实践中,你可以使用任意多个桶,也可以起一个更好的变量名。
class HashMap {
// ...
bucket(key) {
let h = murmur3(key);
return this.bs[
h % this.bs.length
];
}
}
这里的 bucket 方法中对输入的键应用了 murmur3 函数来找应该使用的桶,这是我们整个哈希表程序中唯一用到哈希函数的地方。
class HashMap {
// ...
entry(bucket, key) {
for (let e of bucket) {
if (e.key === key) {
return e;
}
}
return null;
}
}
这里的 entry 方法使用了一个桶和键,扫描这个桶直到找到与键对应的入口。如果找不到入口,则返回 null。
class HashMap {
// ...
set(key, value) {
let b = this.bucket(key);
let e = this.entry(b, key);
if (e) {
e.value = value;
return;
}
b.push({ key, value });
}
}
这里的 set 方法是第一个在先前的 JavaScript Map 示例代码中出现过的方法。它接受一个键值对并将其存储在我们的哈希表中。它调用了我们前面创建的 bucket 和 entry 方法。如果找到了入口,它的值会被覆写;如果未找到,输入的键值对会被添加到表中。在 JavaScript 中,{ key, value } 是 { key: key, value: value } 的简写。
class HashMap {
// ...
get(key) {
let b = this.bucket(key);
let e = this.entry(b, key);
if (e) {
return e.value;
}
return null;
}
}
get 方法与前文的 set 方法很相似。它使用 bucket 和 entry 方法来获取与传入的 key 相对的入口,就像在 set 中做的一样。如果存在入口,返回与输入的键对应的值;如果不存在则返回 null。
这个哈希表实现的代码量不小,其中你必须知道的一点就是:我们的哈希表是一个数组的数组,并且我们使用一个哈希函数来获知一个键值对应该存储的位置。
下面是我们的哈希表实际运行的可视化展示(见原文)。你可以点击任意桶以调用 set 方法添加键值对。为了保持可视化的复杂度,在一个桶“溢出”的时候,所有的桶都会被重置。
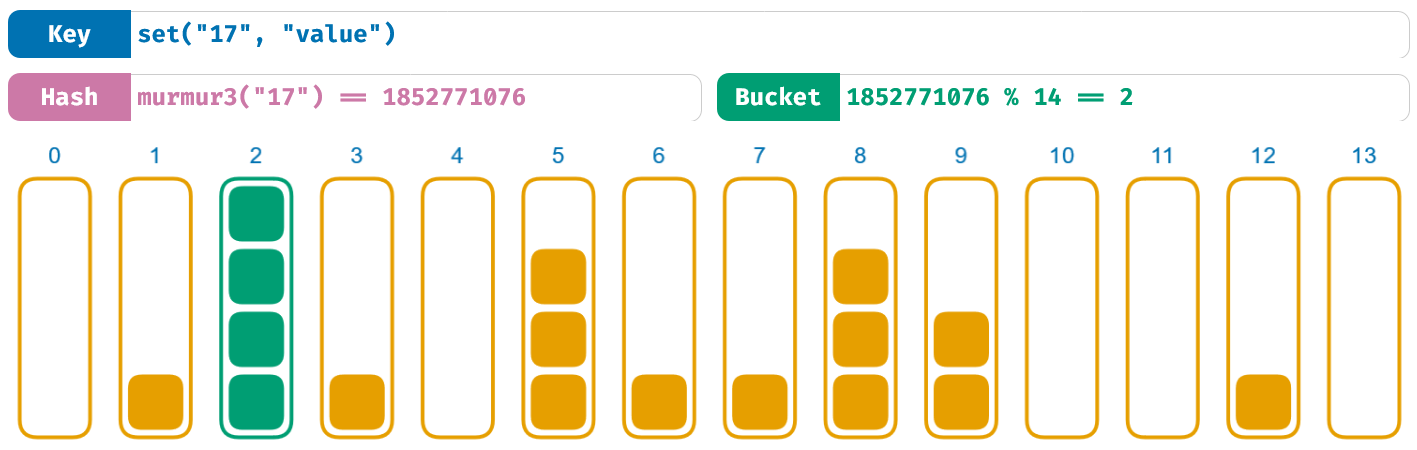
得益于我们使用的 murmur3 哈希函数,你可以通过可视化看到对桶的良好分配。虽然可能仍会一些不均衡,但结果总体上仍是平均的。
要想从哈希表中获取值,我们首先将哈希函数应用于 key 以计算存储着对应值的桶,然后再将需要查找的 key 与桶中所有的 key 进行比较。
这就是在哈希计算过程中我们最小化的查询步骤。并且哈希函数计算得越快,我们就能越块得找到对应的桶,我们的哈希表总体运行得也就越快。
这也是避免哈希碰撞如此重要的原因。如果我们一直使用文章开头的伪哈希函数(即永远返回 0 的函数),我们就会把所有的键值对存到第一个桶中。对于这种哈希函数,查询的性能损耗相比于好的哈希函数是相当高昂的。而使用好的哈希函数,就意味着对每个桶的合理分配,我们就可以把查询操作的时间复杂度降低到 1 / N,这里的 N 是桶的数量。
让我们再看看 stringSum 的表现:
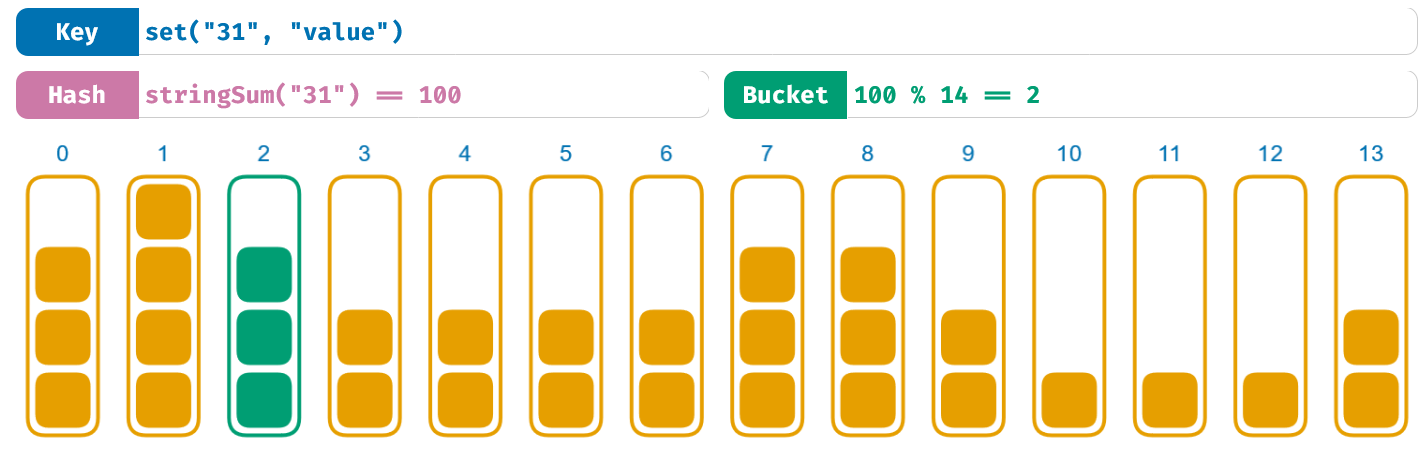
有趣的是,stringSum 似乎可以将值分配得很好。虽然你可以发现一些规律,但这总体的分配看起来很棒。
Haskie:stringSum 终于赢了一回!我就知道它会在某些方面更擅长一些。
还没这么快呢,Haskie。我们还需要考虑更多更复杂的问题。对于这些连续的数字来说,这里的分配做得很好,但是在先前的雪崩效应测试法中,我们之前已经知道,stringSum 的效果并不理想。
生产环境中的哈希碰撞
让我们着眼于两个真实的数据集:IP 地址 和 英语单词。我会将一亿个随机的 IP 地址和 466,550 个英语单词输入到 murmur3 和 stringSum 两个函数中,然后查看分别发生了多少哈希碰撞。
| IP Addresses | ||
|---|---|---|
| murmur3 | stringSum | |
| 哈希碰撞次数 | 1,156,959 | 99,999,566 |
| 碰撞占比 | 1.157% | 99.999% |
| English words | ||
|---|---|---|
| murmur3 | stringSum | |
| 哈希碰撞次数 | 25 | 464,220 |
| 碰撞占比 | 1.157% | 99.999% |
当我们在真实场景中使用哈希表时,我们不会总是存储随机的数据。你可以想象,在真实的服务器中为限速而计算 IP 地址的访问次数,亦或是为了统计单词的起源和流行度统计单词在历史书籍中的出现次数。由于 stringSum 的高哈希碰撞率,它在这些应用场景上的表现很糟糕。
人为制造的哈希碰撞
接下来轮到爆 murmur3 的金币了接下来是一些 murmur3 的坏消息。这并不是由输入的相似性引起的,看看下面这张图(见原文):
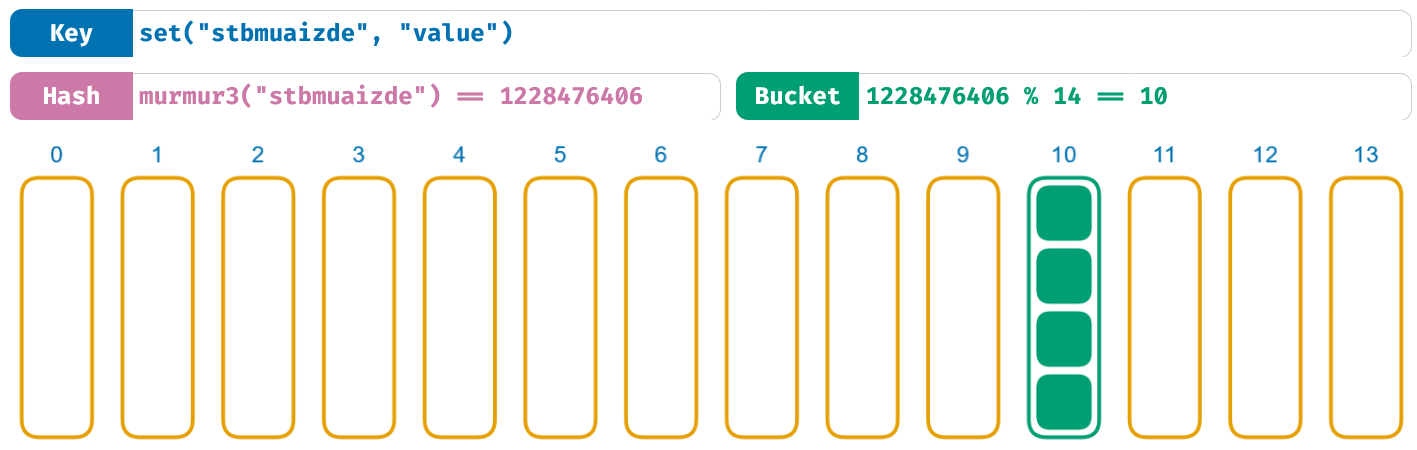
这里发生了什么?为什么这些无意义的单词经过哈希函数后会产生相同的数字?
我穷举了 141 兆(141 万亿)个随机字符串来找出经由 murmur3 产生相同结果(1228476406)的值。由于哈希函数对于一个特定的输入总是能返回同一个输出,所以由暴力出奇迹蛮力来找出哈希碰撞是有可能的。
Haskie:不好意思打断一下,141 兆?141 跟着 12 个零?
是的,而且这只花了我 25 分钟的时间。毕竟计算机很快。
如果你的软件直接使用用户的输入来构建哈希表,在面对不怀好意的人时,后果可能会是毁灭性的。比如,使用 HTTP 头。一个 HTTP 请求看起来会像这样:
GET / HTTP/1.1
Accept: */*
Accept-Encoding: gzip, deflate
Connection: keep-alive
Host: google.com
你不需要完全理解上面这些代码,你只需要知道,第一行是被访问的路径,其它行都是报头就行。HTTP 报头使用键值对的格式,所以 HTTP 服务器一般都会使用表结构来存储这些信息。没有什么能阻止我们传递我们想要的 HTTP 报头,所以我们可以刻意使用特殊的 HTTP 报头来引发服务器的哈希碰撞。这会极大地减慢服务器的运行效率。
这不只是理论上可能发生的。如果你搜索“HashDoS”你能看到很多相关的实际案例。这是个在本世纪初期很重要的安全问题。
存在一些途径来减轻 HashDoS 对服务器的危害,举个栗子,忽略无意义的 HTTP 报头的键和限制存储的 HTTP 报头的数量。但是像 murmur3 这样的现代哈希函数能提供一个更通用的解决方案:随机化。
在这篇文章中,我们已经展示了几个哈希函数的使用例子。这些函数接受一个输入参数。许多现代的哈希函数还有第二个参数:种子(seed,一些时候也称作 salt)。在 murmur3 的例子中,使用的种子是一串数字。在之前,我们都使用 0 作为种子。让我们看看如果使用数字 1 作为种子,还会不会发生前文的哈希碰撞(见原文):
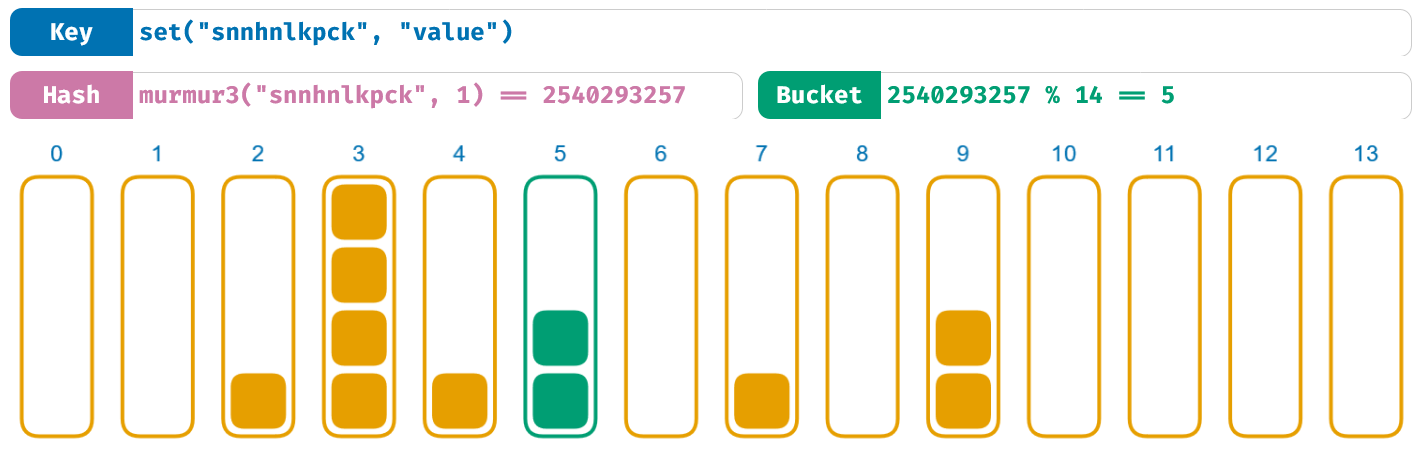
将种子从 0 改成 1,先前的哈希碰撞就消失了。这就是种子的作用:它以不可预计的方式随机化了哈希函数的输出。本文中不讨论种子是如何做到这一点的,不同的哈希函数有不同的实现方式。
对于相同的输入,哈希函数仍然返回相同的输出。只不过,这里的输入结合了 input 和 seed。会在一个种子下引发哈希碰撞的输入不会在另一个种下下引发。一些编程语言中通常在进程开始时使用随机数作为种子,所以当你每一次运行程序时,使用的种子都不同。对于不怀好意的人,如果不知道种子的话,他们很难再造成破坏。
如果你仔细观察了上面的和之前的可视化,你会发现,他们都使用了相同的输入,但是产生了不同的哈希值。这说明,如果你用了一个种子来计算哈希值,并且希望在之后重新计算哈希值进行比较,你需要确保使用相同的种子。
使用不同的种子不会影响哈希表的使用,因为哈希表只存在于程序的运行期间。在程序的生命周期内,哈希表会使用相同的种子进行计算,你的哈希表也就能继续正常工作。如果你将哈希值存储在了程序外部,比如在一个文件中,你需要注意保存你所使用的种子。
测试场
就像以往一样,我为你搭建了一个测试场地。你可以编写你自己的哈希函数,在这里进行可视化,就像在文章中的图片那样。点击这里来试试吧!
结论
我们说明了哈希函数的定义,一些测试哈希函数的途径,不好的哈希函数的表现,还有哈希函数中隐含的安全问题。哈希函数的领域非常广阔,在这篇文章中,我们仅仅只触及了其中一隅。我们还没有提到加密和非加密的哈希算法,我们只接触到了数千种哈希函数的用例中的一种,我们也还没有说明现代哈希函数具体的工作方式。
如果你对这些内容感兴趣并且想要继续深入学习的话,我推荐你阅读下面这些内容:
- https:github.com/rurban/smhasher 这个储存库是用来测试哈希函数好坏的黄金标准。他们使用许多哈希函数运行过大量的测试,并且将结果用大表格展示了出来。要理解所有这些测试方法的目的是很艰难的,但这就是哈希函数测试的现状所在。
- https:djhworld.github.io/hyperloglog/ 这是一个聚焦于
HyperLogLog数据结构的一个交互式的网页。它可以用来在巨大的数据集中高效地计算独一无二的元素的数量。它使用哈希算法用非常巧妙的方式做到了这一点。 - https:www.gnu.org/software/gperf/ 这是一个用来针对你想要进行哈希运算的数据集自动生成“完美”的哈希函数的软件工具。
欢迎加入 Hacker News 上的相关讨论!
鸣谢
感谢阅读了本文草稿并提供珍贵反馈的每一位读者:
还有每一位帮助我找到 murmur3 哈希碰撞数据的朋友: