正交 | Orthogonality
内积 | Inner Product
设向量  与
与  同为 n 维向量,将其看作
同为 n 维向量,将其看作  的矩阵。
的矩阵。
则  与
与  的内积,,即为
的内积,,即为  。
。

一个小例子
范数 / 长度 | Norm / Length
对于一个  的矩阵 v,其范数
的矩阵 v,其范数

- 长度为 1 的向量为单位向量,,
- 将一个向量标准化,,后即可转化为同方向上的单位向量
向量间距离 | Distance
对于向量  与
与  ,其相互距离
,其相互距离

向量正交 | Orthogonal Vectors
对于向量  与
与  ,若其内积为零,则其互相正交。
,若其内积为零,则其互相正交。
毕达哥拉斯定理 | The Pythogorean Theorem
对于两个正交向量,有

正交补 | Orthogonal Complements
对于一个向量 z,有子空间 W,其所有元素均与 z 正交,则 W 为 z 的正交补。
投影 | Projection
要求向量 y 在 u 方向上的投影,有公式

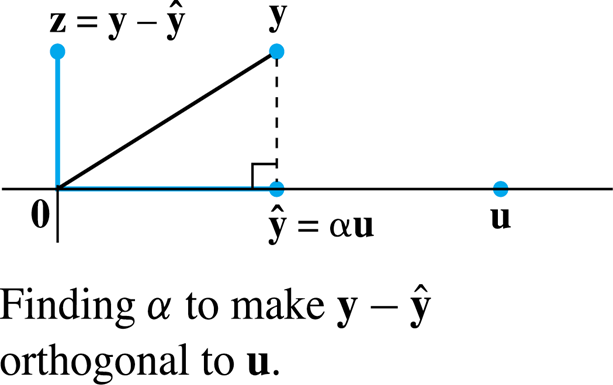
向量在空间上的投影
设有一个向量 y 和一个空间 W,u1 和 u2 为 W 上的一组正交基,则 y 在 W 上的投影为:

斯密特正交化 | Gram-Schmidt Process
给定一组在子空间 W 下的基  ,有
,有

则计算所得  即为 W 下的一组正交基。
即为 W 下的一组正交基。
最小二乘 | Least-Squares
